【演算法】2023 期中考古題解

這是【演算法】課程 2023 年期中考古題的部分題解（與 2025 考試範圍接近的題目），希望能幫助到正在深陷期中地獄的你。

歡迎加入

如果你有任何想要討論的想法，除了在這篇文章底下留言以外，也可以考慮加入 NCHU 電資雲端學院 Discord 伺服器跟我們一起討論！

1. Given an integer array of…

Given an integer array of length n, where one element appears more than $\frac{n}{2}$ times, use divide and conquer to find this element. Prove that the time complexity of your algorithm is $O(nlogn)$. In your answer, include:

1. The process of how you used divide and conquer to solve this problem.

2. The method you used to calculate the time complexity of the algorithm.

3. Prove that the time complexity of your algorithm is $O(nlogn)$

4. An example to demonstrate how your algorithm works for this problem.

$\because$ 要使用 divide and conquer $\therefore$ 我們使用 merge sort 先對原陣列進行排序。

接著我們遍歷排序後的陣列，當遇到相同元素就 count++，當 count 超過陣列元素數量的一半就找到目標了：

1
2
3
4
5
6
7
8
9

for(int index = 1, count = 1; index < arr.length(); index++) {
  if (arr[index-1] != arr[index])
    count = 1; // 遇到新的數值，重置成 1 個
  else
    count++; // 遇到一樣的數值

  if (count > n/2)
      return arr[index];  // 過半數量個相同的元素
}

估計時間複雜度：因為 merge sort 是 $O(n logn)$，for 迴圈遍歷一輪是 $O(n)$，所以總時間複雜度是 $O(n logn)$

舉例說明：

1. 原數列 arr 為 2132221
2. 進行 merge sort，得到 1122223
3. 開始遍歷：

1
2
3
4
5
6

index = 1: count = 2
index = 2: count = 1
index = 3: count = 2
index = 4: count = 3
index = 5: count = 4
# 過半，答案為 arr[index] == 2

2. Order the following functions…

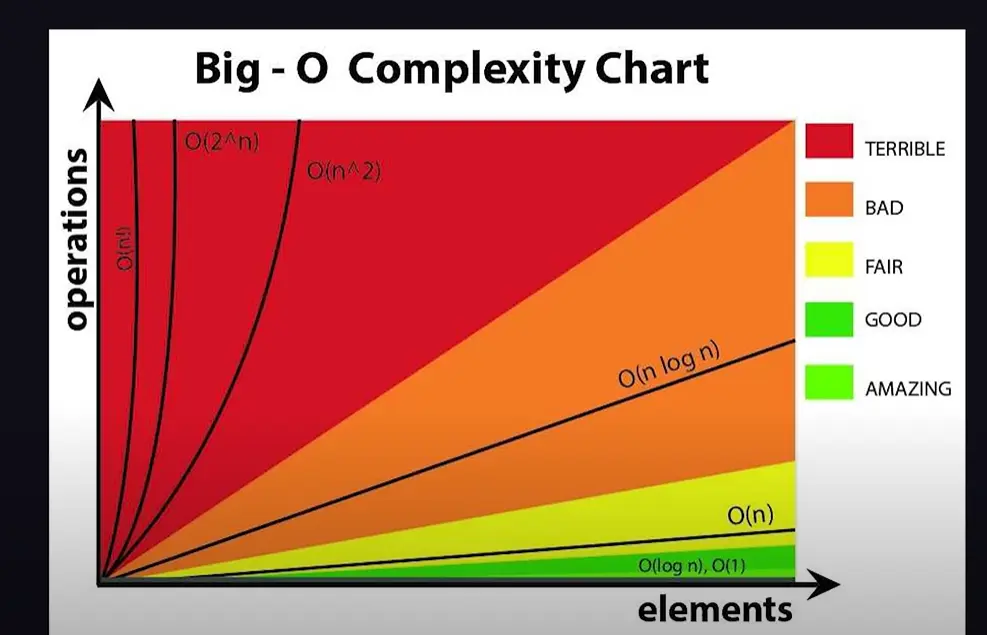
Order the following functions according to big $O$ notation, from smallest to largest: $f(n)=n^2$, $g(n)=log(n)$, $h(n)=nlog(n)$, $j(n)=2^n$

可以參考這張圖（來源） ：

$Ans:\log n\to n\log n\to n^2\to2^{n}$

3. What is sleep sort?

What is sleep sort?

對將陣列中的元素分別使用線程 sleep 等待，越小的數會等待越少的時間並 return，就能得到排序後的結果。

以 Go 語言為例，程式碼：（考試應該不用寫 Code 這段）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

package main

import (
   "fmt"
   "time"
)

func printAfter(second int) {
   time.Sleep(time.Duration(second) * time.Second) // 等待 second 秒
   fmt.Print(second) // 印出數字
}

func main() {
   arr := []int{3, 8, 9, 2, 1, 7}
   for _, v := range arr {
      go printAfter(v) // 開一個 goroutine 執行 printAfter
   }

   time.Sleep(time.Duration(10) * time.Second)
}

4. Suppose you have a sequence of…

Suppose you have a sequence of $n$ positive integers, where the numbers are not necessarily ordered in inscreasing or decreasing order. You need to write an algorithm to find the first duplicate number in the sequence. Design an algorithm with a time complexity of $O(nlogn)$ to solve this problem.

我們可以設計一個資料結構 pair: (value, index)，value 代表原 array 中的值、index 代表出現在 array 的何處。

接著我們遍歷一次 array，將 array 轉換為由我們的資料結構組成的陣列（花費 $O(n)$）

example: array: [3, 1, 4, 1, 5, 9, 2, 6, 5]，則轉換後為 new_array: [(3, 0), (1, 1), (4, 2), (1, 3), (5, 4), (9, 5), (2, 6), (6, 7), (5, 8)]

然後將轉換以後的 new_array 進行排序，先排 value 再排 index（merge sort，$O(nlogn)$）

接著兩兩、由左至右進行比較，若 value 相同時查看 index 是否比原本記憶的 min_index 小（如果比較小就代表這是「更早」出現的 duplicate number）

1
2
3
4
5
6
7

for(int index = 1, min_index = Integer.MAX_VALUE, min_value = 0; index < new_array.length(); index++) {
  if ((new_array[index-1].value == new_array[index].value) && (index < min_index)) {
	min_index = index;
  	min_value = new_array[index].value;
  }
}
return min_value;

5. In shell sort, the gap…

In shell sort, the gap sequence determines:

(a). The number of swaps required to sort the list

(b). The number of comparisons required to sort the list

(c). The order in which the sub-lists are sorted

(d). The running time of the algorithm

(e). The stability of the sorting processing

一個一個來：

✔(a). 排序過程中需要的交換次數

間隔 h 會影響到切割出子陣列的數量、進而影響需要的 swaps 次數。

✔(b). 排序過程中需要的比較次數

同 (a)，會影響需要做的比較次數。

✖(c). 子列表排序的順序

根據老師提供的實作程式碼（LECTURE 4: ELEMENTARY SORTING ALGORITHM P.134）：

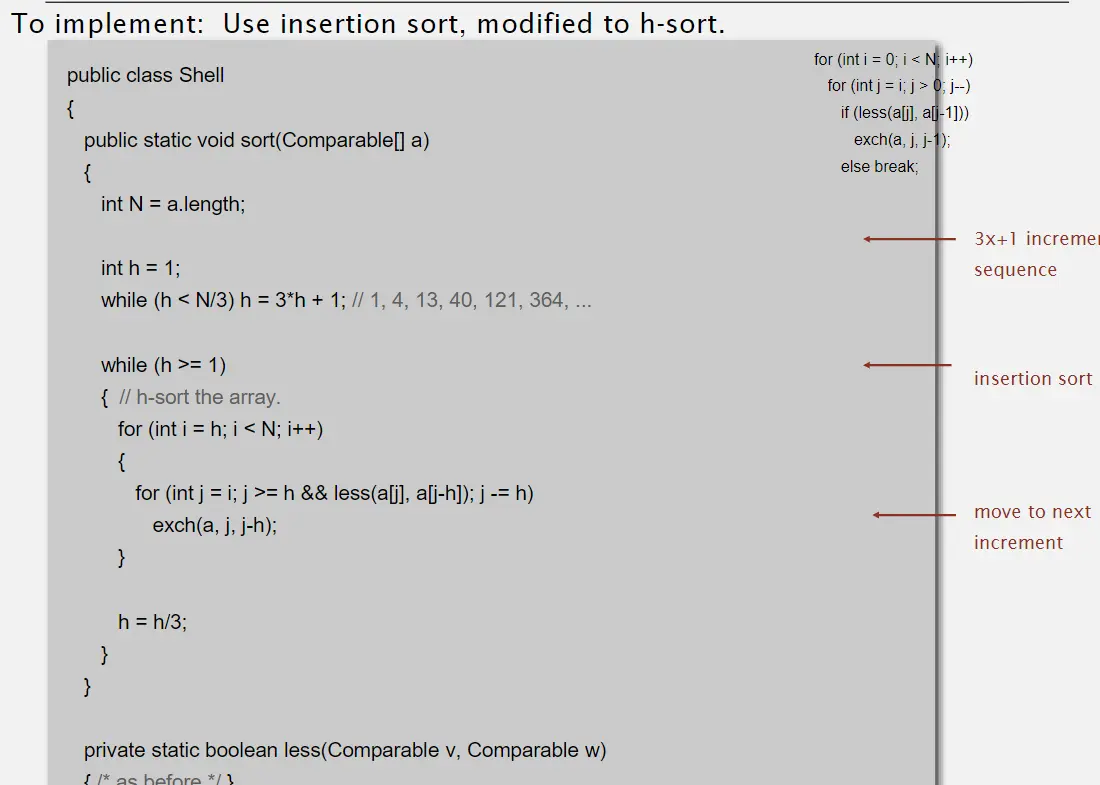
可以看到並不是「排序完一個子陣列再開始排下一組」，而是「按照索引，對該索引的元素所屬的子陣列向前進行 insertion sort」

舉例來說當 index 走到 7，h 是 3，那麼排序好的只有 index = 0, 3, 6、index = 1, 4, 7、index = 2, 5, 8 三個部分（分別排好），任何 index > 7 的部分都還是亂的。

所以與 h 不直接相關。

✔(d). 演算法的執行時間

同 (a)、(b)。

✖(e). 排序過程的穩定性

Shell sort 本身就是 unstable 排序，與 h 無關。這是因為 Shell sort 在進行遠距離元素交換時，可能會改變相等元素的相對順序。

6. Which of the following is NOT TRUE…

Which of the following is NOT TRUE about shell sort?

(a). Shell sort is an in-place algorithm

(b). Shell sort requires less memory than insertion sort.

(c). The time complexity of shall sort in the worst case is $O(n^2)$

(d). Shell sort is a divide-and-conquer algorithm

題目問關於 shell sort 何者為 FALSE？

TRUE (a). Shell sort 是 in-place 排序

Shell sort 是 insertion sort + 切割，但它跟 insertion sort 一樣都是 in-place 排序。

FALSE (b). Shell sort 比起 insertion sort 只需要更少的記憶體

Shell sort 是在 insertion sort 的基礎上加上「先分割為子陣列」，需要消耗額外的記憶體來儲存像是 h（gap）的值。

TRUE (c). Shell sort 在最壞情況下的時間複雜度是 $O(n^2)$

Shell sort 的最壞時間複雜度取決於 gap sequence 的選擇。使用 Knuth 序列（1, 4, 13, 40, …）時，最壞情況下的時間複雜度為 $O(n^{3/2})$，但某些 gap sequence 下可能達到 $O(n^2)$。

FALSE (d). Shell sort 是 divide-and-conquer 排序

divide-and-conquer 的 conquer 會用到遞迴來合併子問題的解，shell sort 沒用到。

7. Suppose you have a list of…

Suppose you have a list of $n$ elements, and you want to generate a random permutation of this list using the Knuth shuffle algorithm. What is the expected number of swaps required to generate the random permutation?

根據 LECTURE 4: ELEMENTARY SORTING ALGORITHM P.182 的程式碼：

在 for 迴圈中，每一輪都會讓第 i 個元素與 StdRandom.uniform(i+1) 的元素做交換 1 次。

我們共有 n 個元素，所以共交換 n 次。

8. What is the advantage and disadvantage…

What is the advantage and disadvantage of the weighted-quick-union with path compression implementation over the quick-find implementation of the union-find algorithm? Please compare them in terms of time complexity and memory usage.

Weighted quick union with path compression 下稱 WQU-PC；Quick-find 下稱 QF。

WQU-PC 的優勢：樹高被限制在 $log(N)$，並且樹高還能在經過多次查詢後，被 path compression 再壓低至 $lg*(N)$

WQU-PC 的劣勢：Find 時需找 root，不如 QF 只要 $O(1)$

Time complexity of Find: QF 直接查看 id 只需要 $O(1)$；WQU-PC 最少需要 $lg*(N)$。

Time complexity of Union：QF 需要 $O(N)$；而 WQU-PC 雖然需要在 Union 時進行兩次 find 操作，但在 path compression 後，樹高可以壓到 $lg*(N)$，所以時間複雜度優於 QF。

Memory usage：QF 需要一個大小為 N 的 id[] 陣列，空間複雜度為 $O(N)$；WQU-PC 需要一個大小為 N 的 id[] 陣列和大小為 N 的 size[] 陣列，空間複雜度同樣為 $O(N)$。

9. Consider the following list…

Consider the following list of integers: [7, 2, 4, 1, 3, 6, 5, 8]. How many inversions are in the lists?

題目說的 inversion 指的是前大後小的數字組合。也就是對於索引 i < j，若 array[i] > array[j]，則稱 (array[i], array[j]) 為一個 inversion。

答：共 10 個 inversion，分別為：

1. (7, 2)
2. (7, 4)
3. (7, 1)
4. (7, 3)
5. (7, 6)
6. (7, 5)
7. (2, 1)
8. (4, 1)
9. (4, 3)
10. (6, 5)

10. In theory, Merge Sort has better…

In theory, Merge Sort has better time complexity than Quick Sort. However, why is Quick Sort often faster than Merge Sort in practice?

Quick sort 相比於 merge sort 有著較少的搬移、in-place 移動的優成，而且實做中我們也會利用先把陣列隨機打亂、三數取中法（見 Lecture 6: Quick Sort Algorithm P.40）來避免選到 worst 的 pivot。這導致 Quick sort 經常比 Merge sort 還要快速。

11. Given the following merge…

Given the following merge sorting algorithm (Figure 1), please comments on the algorithm from the perspective of best-case time complexity, worst-case time complexity, stable property, and in-place property.

這題會用到的講義資料可參考：

1. LECTURE 5: MERGE SORTING ALGORITHM P.32
2. LECTURE 5: MERGE SORTING ALGORITHM P.50

答：

這是一個 top-down 的 merge sort，in-place 的 insertion 合併。

Best-case time complexity: 當 sub-array 已經排好時，最佳效能 $O(\frac{1}{2}NlogN)$, swap = 0 因為仍然有做 divide 的動作，有 $logN$ 層；每層都需要做 $N/2$ 次比較。

Worst-case complexity: 當左 sub-array 都大於右 sub-array 時，每次 insertion 都需要移動前面的元素，時間複雜度為 $O(N^2logN)$。

Stable proterty: 因為使用 insertion 合併，故與 insertion sort 的特性一樣，是 stable。

In-place property: 它使用 i, j index 讓 array merge，並沒有使用另一個 array 來做 merge，所以是 in-place 的演算法。

12. Suppose you have a dynamic…

Suppose you have a dynamic data structure that uses a resizing array to store its elements. The array starts with a size of $1$, and each time it becomes full, it is resized to twice its current size. You insert $n$ elements into the data structure, and each insertion takes $O(1)$ time.

For showing the total time complexity of inserting $n$ elements into the data structure, we have the following statements:

• Each insertion takes $O(1)$ time, so inserting $n$ elements takes $O(n)$ time.

• The array starts with a size of $1$, and each time it becomes full, it is resized to twice its current size. This means that the array is resized $log_2(n)$ times, since the array doubles in size each time it is resized.

• The total time complexity of resizing the array is $O(nlog_2(n))$, since each resize takes $O(n)$ time and the array is resized $log_2(n)$ times.

• Therefore, the total time complexity of inserting $n$ elements into the data structure is $O(n+nlog_2(n))=O(nlog_2(n))$

1. 正確
2. 正確
3. 錯誤，Resize 每次的成本與當下的陣列大小成正比，而不是每次都 $O(N)$，總成本應該是 $1+2+4+8+\cdots+\frac{n}{2} = n-1$（等比級數和）
4. 錯誤，應該為 $O(N+N)=O(N)$